Предположим, что футбольная команда вашей школы участвует в соревнованиях и играет с командами других школ. Пусть общее число команд равно шести. Вашу команду обозначим буквой А, а другие команды — буквами B, C, D, E и F. Через несколько недель после начала соревнований окажется, что не­которые из команд уже сыграли друг с другом, например:
A с C, D, F;
B c C, E, F;
С с A, B;
D с A, E, F;
E с B, D, F;
F с A, B, D.

Это можно изобразить при помощи такой геометрической схемы. Каждую команду представим точкой или маленьким кружочком и соединим отрезком те пары точек, которые соответствуют командам, уже игравшим друг с другом. Тогда для данного списка проведенных игр мы получим схему, изображенную на рис. 5.

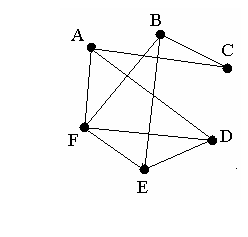
рис. 1

Схема такого вида называется графом. Она состоит из нескольких точек А, В, С, D, E, F,называемых вершинами, и нескольких соединяющих эти точки отрезков, таких, как АС или ЕВ, называемых ребрами графа.

Итак, фигуру, образованную набором точек и отрезков, соединяющих некоторые из этих точек, называется графом. Точки называются вершинами графа. А отрезки – ребрами графа.

Примерами графов могут служить схемы метрополитена, железных и шоссейных дорог, планы выставок и т.д. С помощью графов указываются различные связи между объектами.

Из рис. 5 видно, что точки пересечения некоторых ребер графа могут не являться его вершинами; это происходит потому, что мы изобразили наш граф на плоскости. Возможно, удобнее было бы представлять себе его ребра нитями, проходящими друг над другом в пространстве; во всяком случае, при изображении на плоскости вершины графа во избежание путаницы должны отмечаться достаточно отчетливо (например, кружочками).

Один и тот же граф может выглядеть на рисунках по-разному. Например, на трех рисунке 6 (а), (б), (в), мало похожих друг на друга, изображен один и тот же граф. Три этих графа имеют одинаковое число вершин, и соответствующие вершины графов соединены ребрами.

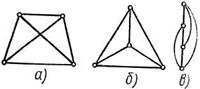
рис. 6

Задача 1.1. Рассмотрим следующие рисунки. Изображают ли они один и тот же граф?
А)

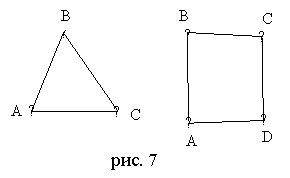
1. Проверим число вершин на графах.
В первом графе три вершины, а во втором четыре, следовательно, графы разные.
B)

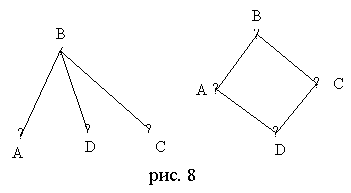
1. Проверим число вершин на графах.
В первом и во втором графе по четыре вершины.

2. Проверим, соединены ли ребрами соответствующие вершины графа.
Вершина А в первом графе соединена только с вершиной В. А во втором графе вершина А соединена еще и с вершиной D. Следовательно графы разные.

Задача 1.2. Аркадий, Борис, Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?
Решение:
Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию – отрезок или часть кривой, соединяющая конкретные точки – имена.
Рассмотрим процесс соединения точек А, Б, В, Г, Д ребрами.
1. Ситуация, соответствующая моменту, когда рукопожатия еще не совершались, представляет собой точечную схему, изображенную на рис 3.  Такую схему называют нулевым графом.
                                  
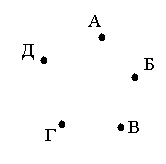
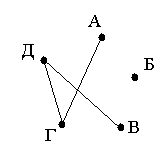
Рис 9.                                                            Рис 10.
2. Ситуация, соответствующая моменту, когда совершены еще не все рукопожатия, может схематически быть изображена, например, с помощью рис. 10.
Графы, в которых построены не все возможные ребра, называются неполными графами.
3. На рис. 9 Борис не сделал ни одного рукопожатия. Вершины, которые не принадлежат ни одному ребру, называются изолированными.
Теперь мы можем тать четкое определение нулевому графу. Схема, состоящая из «изолированных» вершин, называется нулевым графом.
4. Ситуация, когда осуществились все рукопожатия, изображена на рис. 11. В нем каждая из вершин соединена с каждой из оставшихся. Этот граф называется полным графом.

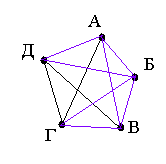
Рис 11.
Если мы подсчитаем число ребер графа, изображенного на рис. 11, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10.
Заметим, что граф, не являющийся полным, можно дополнить до полного с теми же вершинами, добавив недостающие ребра. Так на рис. 10 изображен неполный граф с пятью вершинами. А на рис. 11 граф превращен в полный. Ребра, превращающие граф в полный изображены фиолетовым цветом. Совокупность вершин графа с этими ребрами называется дополнением графа.
Предложение 1. Докажем, что если полный граф имеет n вершин, то количество ребер  будет равно: .
Действительно, всего вершин n штук, каждая соединена с n-1 вершиной – получаем произведение n(n-1). Но мы посчитали каждое ребро два раза, значит, надо произведение разделить на два, и тогда получим искомую формулу для нахождения количества ребер.
Задача 1.3. Существует ли полный граф с семью ребрами?
Решение. Допустим, что такой граф существует.
Зная количество ребер, узнаем количество вершин.
=7; n(n-1)=14.

Заметим, что n и (n-1) – это два последовательных натуральных числа. Число 14 не6льзя представить в виде произведения двух последовательных натуральных чисел, значит, данное уравнение не имеет решений. Следовательно, такого графа не существует.