Задача 8.1. Шесть школьников участвуют в шахматном турнире, который проводится в один круг, т. е. каждый шахматист встречается со всеми участниками по одному разу. Докажите, что среди них всегда найдутся три участника турнира, которые провели уже все встречи между собой или еще не сыграли друг с другом ни одной партии.
Решение. Любые два участника турнира непременно на­ходятся между собой в одном из двух отношений: они либо уже сы­грали между собой, либо еще не сыграли.
Каждому участнику поставим в соответствие вершину графа. Соединим вершины попарно ребрами двух цветов. Пусть ребро крас­ного цвета означает, что двое уже сыграли между собой, а синего — что не сыграли. Получим полный граф с шестью вершинами и ребрами двух цветов.
Теперь для решения задачи достаточно доказать, что в таком графе обязательно найдется «треугольник» с одноцветными сто­ронами.
Каждая вершина нашего графа принадле­жит пяти ребрам. Скольким ребрам" одного цвета может принадлежать произвольная вершина такого графа? Пять принадлежа­щих одной вершине ребер могут быть ок­рашены без учета порядка следующим образом (Красное ребро обозначим буквой к, синее - с): ссссс; ксссс; ккссс; ккксс; ккккс; ккккк.
                                              
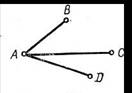
                                                    Рис 49.

То есть каждая вершина принадлежит, по меньшей мере, трем ребрам одного цвета. Пусть, например, вершина А принадлежит трем ребрам красного цвета (рис. 49). Ка­кого цвета ребра могут соединять вершины
В, С и D?

                                                 
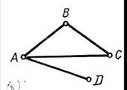
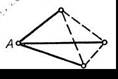
Рис. 50                                              рис. 51

Если хотя бы одно из них окажется красным, как на рисунке 50, то получится треугольник с красными сторонами. Если же все эти ребра синие, как на рисунке 51, то они вместе образуют «треугольник» с синими сторонами.
Задача решена. Рассмотрены все возможности; в каждом случае нашлись три шахматиста, или все сыгравшие между собой по одной партии, или не сыгравшие между собой ни одной партии.
Кроме того, при ее решении доказаны два свойства таких графов.
Свойство 1. Любая вершина полного графа с шестью или более вершинами и ребрами двух цветов принадлежит, по меньшей мере, трем ребрам одного цвета.
Свойство 2. В любом полном графе с шестью или более вершинами и ребрами двух цветов найдется, по меньшей мере, один треугольник с одноцветными сторонами.
Задача 8.2.
На географической карте выбраны пять горо­дов. Известно, что среди них из любых трех найдутся два, соединен­ные авиалиниями, и два — несоединенные.
Докажите, что тогда: 1) каждый город соединен авиалиниями непосредственно с двумя и только с двумя другими городами; 2) вылетев из любого города, можно облететь остальные, побывав в каждом по одному разу, и вернуться назад.
Решение. И в этой задаче рассматриваются множество объ­ектов—городов и два отношения, заданные для элементов этого мно­жества; каждые два города находятся в одном из двух отношений — они либо соединены между собой авиалиниями, либо не соединены. Пусть вершины графа соответствуют городам: красное ребро — наличию авиалинии, синее— отсутствию.

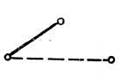
Рис. 52
По условию среди трех ребер, соединяющих любые три вершины, одно — красное, второе — синее (рис. 52), а это означает, что в графе нет ни одного треуголь­ника с одноцветными сторонами. Тогда из решения предыдущей задачи следует, что каждая вершина непременно принадлежит двум красным ребрам и двум синим, поскольку в против­ном случае образовался бы треугольник с одноцветными сторона­ми. А это и означает, что каждый город соединен авиалиниями с двумя и только с двумя городами.
Остается показать, что в графе найдется «пятиугольник», все ребра которого — красные.
                                   
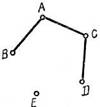
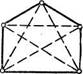
Рис. 53                                         рис. 54
Выберем одну из вершин, например А, а красными будут, скажем, ребра (А, В) и (А, С) (рис. 53).
Ребро (В, С) (рис. 53) не может быть красным, следовательно, красным является одно из ребер: либо (С, D), либо (С, E). Пусть красное (С, D). Если теперь соединить красным ребром вершины D и В, то вершина Е должна быть соединена красными ребрами с вершинами, которые принадлежат уже двум красным ребрам. По условию это невозможно. Остается соединить красными ребрами вершины D и Е, В и Е. Остальные ребра должны быть синими (рис. 54).
Итак, получим еще одно свойство.
Свойство 3. Если в полном графе с пятью вершинами и ребрами двух цветов не найдется треугольника с одноцветными сто­ронами, то граф можно изобразить в виде «пятиугольника» с крас­ными сторонами и синими диагоналями.
Задача 8.3.
В течение дня двое из шести телефонных або­нентов могут, очевидно, поговорить друг с другом по телефону, а могут и не поговорить. Докажите, что всегда можно указать две тройки абонентов, в каждой из которых все переговорили друг с другом или все не переговорили.
Решение. Пусть у полного графа с шестью вершинами крас­ные ребра соответствуют парам абонентов, которые говорили друг с другом по телефону, синие — тем, кто не говорил.

                                                          
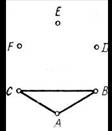
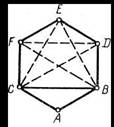
Рис. 55                                             рис. 56

Тогда в графе найдется хотя бы один треугольник, например АВС с од­ноцветными сторонами (рис. 55). Остает­ся показать, что обязательно найдется еще и второй такой треугольник.
Временно исключим из рассмотрения одну из его вершин, скажем А, вместе с ребрами, принадлежащими ей.
Найдется ли в оставшемся графе с пя­тью вершинами треугольник с одноцвет­ными сторонами? Если найдется, то он со­держится и в исходном графе.
В противном случае получается пяти­угольник с красными сторонами и синими диагоналями (рис. 56). Теперь восстано­вим шестую вершину А с ее ребрами (рис. 55). Если ребро (А, D) или ребро (А, F) будет окрашено в красный цвет, то образуется еще минимум один треугольник с красными сторонами ADB или ACF. Если оба эти ребра будут синего цвета, то появится треугольник AFD с синими сторонами. Вывод нетрудно перевести с языка теории графов на язык задачи.
Установлено свойство графа, являюще­еся обобщением   свойства 2.
Свойство 4. В любом полном графе с шестью или более вершинами и ребрами одного из двух цветов всегда найдутся два разных треугольника с одноцветными сто­ронами. Эти два треугольника могут иметь общую вершину или даже общее ребро.
Задача 8.4.
Каждый из семнадцати ученых переписывается с остальными. В их переписке речь идет лишь о трех темах. Каждая пара ученых переписывается друг с другом лишь по одной теме. Докажите, что не менее трех ученых переписываются друг с другом по одной и той же теме.
Решение. Условию задачи соответствует полный граф с семнадцатью вершинами и ребрами трех цветов. Из каждой вершины выходят шестнадцать ребер. Докажем, что в таком графе найдется хотя бы один треугольник с одноцветными сторонами. Заметим, что каждая вершина этого графа принадлежит хотя бы шести реб­рам одного цвета. (Докажите это самостоятельно.) Пусть, напри­мер, вершина А принадлежит шести красным ребрам (рис. 57).

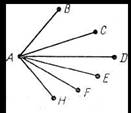
Рис. 57

Если среди вершин В, С, D, E, F, Н найдутся две, которые сое­динены красным ребром, то получится треугольник с красными сто­ронами. Если не найдутся, то все шесть вершин В, С, D, E, F, Н соединены между собой попарно ребрами двух цветов (зеленым и синим). По свойству 2 в этом графе с шестью вершинами найдется хотя бы один треугольник либо с синими, либо с зелеными сторо­нами. Задача решена.
Сформулируем теперь свойство, доказанное при решении этой задачи.
Свойство 5. В полном графе с семнадцатью или более вер­шинами и ребрами трех цветов всегда найдется, по меньшей мере, один треугольник с одноцветными сторонами.
Упражнения для домашнего задания.
1. Докажите, что в полных графах с восемью вершинами и ребрами двух цветов каждая вершина принадлежит по меньшей мере четырем ребрам одного цвета.
2. Докажите, что если каждый из пяти человек переписывается только с двумя другими, то не найдется трех человек, которые все переписываются между собой. Сформулируйте соответствующее свойство.

3. На одном из фестивалей  встретились шесть делегатов.  Оказалось,
что из любых троих, по меньшей мере, двое могут объясниться на одном из языков. Докажите, что найдутся три делегата, каждый из которых может объ­ясниться с каждым из этой тройки. Сформулируйте соответствующее свойство.