Вершины в графе могут отличаться друг от друга тем, скольким ребрам они принадлежат.
Степенью вершины называется число ребер графа, которым принадлежит эта вершина.
Обозначать степени вершин А, В, Сбудем соответственно так: d(А), d(В), d(С) и т. п.
Задача 2.1.
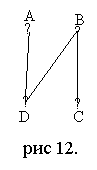
а) Найдите степени вершин А, В, С и D.
Ответ: степ.А=1; степ.В=2; степ.С=1; степ.D=2.
                                                  
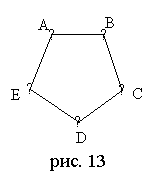
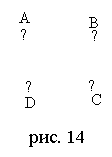
б) Чему равна степень каждой вершины?
Ответ: 2
в) Чему равна степень каждой вершины?                                  
          Ответ: 0.
Степень изолированной вершины равна 0.
Вершина называется нечетной,если ее степень — число не­
четное. Вершина называется четной,если ее степень — число
четное.
Задача 2.2. Уезжая из летнего лагеря, подружившиеся ребята обменялись конвертами с адресами. Докажите, что
а)       всего было передано четное число конвертов;
б)       число участников, обменявшихся конвертами нечетное чис­ло раз, четное.
Решение. Пусть участники слета А1, А2, A3,,... Ап - вершины графа, а ребра соединяют на рисунке 15 пары вершин, изобра­жающих ребят, обменявшихся конвертами:
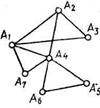                                          рис. 15
а) степень каждой вершины Ai показывает число конвертов, которые передал участник Аi своим знакомым. Общее число переданных кон­вертов N равно сумме степеней всех вершин графа. N = степ. А1+степ. А2+...+степ. Ап-1+ степ. Ап, но N = 2р, где р — число ре­бер графа, то есть N — четное. Следовательно, было передано четное число конвертов.
б) в равенстве N = степ. А1 + степ. А2 + ... + степ. Ап-1 + степ. Ап сумма нечетных слагаемых должна быть четной, а  это может быть только в том случае, если число нечетных слагаемых четно. А это означает, что число участников, обменявшихся кон­вертами нечетное число раз, четное.
В ходе решения задачи 1 доказаны два свойства.
Свойство 1. В графе G сумма степеней всех его вершин — число четное, равное удвоенному числу ребер графа.
степ. А1 + степ. А2+ ... + степ. Аn = 2р,
где р — число ребер графа Г, n — число его вершин.
Свойство 2. Число нечетных вершин любого графа четно.
Задача 2.3. Девять шахматистов проводят турнир в один круг (каждый из участников должен сыграть с каждым из осталь­ных по одному разу). Покажите, что в любой момент найдутся двое, закончившие одинаковое число партий.
Решение. Переведем условие задачи на язык графов. Каж­дому из шахматистов поставим в соответствие вершину графа, со­единим ребрами попарно вершины, соответствующие шахматистам, уже сыгравшим между собой партию. Получим граф с девятью вер­шинами. Степени его вершин равняются числу партий, сыгранных соответствующими игроками. Покажем, что во всяком графе с де­вятью вершинами всегда найдутся хотя бы две вершины одинаковой степени.
Каждая вершина графа с девятью вершинами может иметь сте­пень, равную 0, 1, 2, ..., 7, 8. Предположим, что существует граф G, все вершины которого имеют разную степень, т. е. каждое из чисел последовательности 0, 1, 2, ..., 7, 8 является степенью одной и только одной из его вершин. Но этого не может быть. Действитель­но, если в графе есть вершина Астепени 0, то в нем не найдется вер­шина Всо степенью 8, так как эта вершина В должна быть соедине­на ребрами со всеми остальными вершинами графа, в том числе и с А. Иначе говоря, в графе с девятью вершинами не могут быть одновременно вершины степени 0 и 8. Следовательно, найдутся хотя бы две вершины, степени которых равны между собой.
Вернемся к задаче. Доказано, что в любой момент найдутся хотя бы двое, сыгравшие одинаковое число партий.
Решение этой задачи почти дословно повторяется в ходе дока­зательства следующего свойства (только число 9 приходится заменить произвольным натуральным числом n ? 2).
Свойство 3. Во всяком графе с n вершинами, где n ? 2, всегда найдутся, по меньшей мере, две вершины с одинаковыми сте­пенями.
Задача 2.4. Девять человек проводят шахматный турнир в один круг. К некоторому моменту выясняется, что в точности двое сыграли одинаковое число партий. Докажите, что тогда либо в точности один участник еще не сыграл ни одной партии, либо в точности один сыграл все партии.
Решение: Условие задачи переведем на язык графов. Пусть вершины графа — игроки, а каждое ребро означает, что соответ­ствующие игроки уже сыграли между собой партию. Из условия известно, что в точности две вершины имеют одинаковые степе­ни. Требуется доказать, что в таком графе всегда найдется либо только одна изолированная вершина, либо только одна вершина степени 8.
В общем случае у графа с девятью вершинами степень каждой вершины может принимать одно из девяти значений: 0, 1, 2, ..., 7, 8. Но у такого графа степени вершин принимают только восемь разных значений, ибо ровно две вершины имеют одинако­вую степень. Следовательно, обязательно либо 0, либо 8 будет значением степени одной из вершин.
Докажем, что в графах с девятью вершинами, из которых в точности две имеют одинаковую степень, не может быть двух вершинстепени 0 или двух вершин степени 8.  Допустим, что все же найдется граф с девятью вершинами, в котором ровно две вершины изолированные, а все остальные имеют разные между собой степени. Тогда, если не рассматривать эти две изолированные вершины, останется граф с семью вершинами, степени которых не совпадают. Но такого графа не существует (см. свойство 3). Значит, это предположение неверное.
Теперь допустим, что существует граф с девятью вершинами, в котором ровно две вершины имеют степень 8, а все остальные — несовпадающие степени. Тогда в дополнении данного графа ровно две вершины будут иметь степень 0, а остальные попарно различ­ные степени. Этого тоже не может быть (свойство 3), т. е. и второе предположение неверное.
Следовательно, у графа с девятью вершинами, из которых в точности две имеют одинаковую степень, всегда найдется либо одна изолированная вершина, либо одна вершина степени 8.
Вернемся к задаче. Как и требовалось доказать, среди рассмот­ренных девяти игроков либо только один еще не сыграл ни одной партии, либо только один сыграл уже все партии.
При решении этой задачи число 9 можно было заменить любым другим натуральным числом n > 2.
Это решение поможет вам провести доказательство следующего свойства:

Свойство 4. Если в графе с n вершинами (n > 2) в точно­сти две вершины имеют одинаковую степень, то в этом графе всег­да найдется либо в точности одна вершина степени 0, либо в точ­ности одна вершина степени n - 1.