Задание 4.1. Попробуйте обвести изображения графов на рисунке 22, не отрывая карандаша от бумаги и не проходя уже по обведенному ребру вторично.

                                       
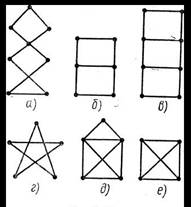
рис. 22

Задание по обведению ребер удается выполнить для графов на рисунках 22 (а, б, г, д). Графы на рисунках 22 (в, е) нарисо­вать без отрыва карандаша от бумаги или, не проходя дважды по ребрам, не удастся. В чем секрет? Какие свойства графа повлияли на это? Для удобства введем специальные понятия.
Перед этим рекомендуется вспомнить с учащимися определения пути и цикла.
Эйлеровым путем в графе называется путь, содержащий все ребра графа.
Эйлеровым циклом в графе называется цикл, содержащий все ребра графа
Граф, обладающий эйлеровым циклом, называется эйлеровым графом.
Принято всякую замкнутую линию, если ее можно начертить, не отрывая карандаша от бумаги, проходя при этом каждый уча­сток в точности один раз, называть уникурсальной.
Теперь заглянем в прошлое. Далее показываем презентацию об Эйлере и знаменитой задаче о Кенигсбергских мостах.
Задача 4.1. В г. Кёнигсберге (ныне Калининград) было семь мостов через реку Прегель (рис. 23, где Л - левый берег, П - правый берег, А и Б - острова). Можно ли, прогуливаясь по берегам реки, пройти по каждому мосту ровно один раз?
        
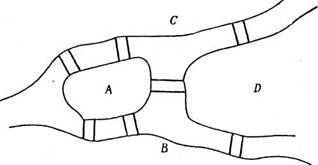
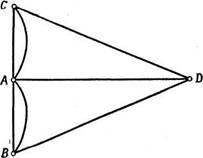
Рис.   23                                                Рис. 24
На рисунке 24 изображен граф, соответствующий задаче о кёнигсбергских мостах. Докажем, что этот граф не является уникурсальным.
Задача 4.2.
Шесть островов на реке в парке "Лотос" соединены мостами.

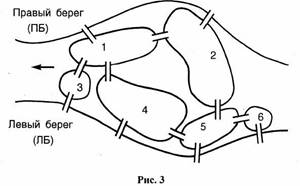
рис. 25
Можно ли, начав прогулку на одном из островов, пройти по каждому из мостиков ровно один раз и вернуться на тот же остров? В случае отрицательного ответа определите, сколько мостиков и между какими островами нужно построить, чтобы такая прогулка стала возможной.
Решение.
Построим граф G, в котором каждому участку суши поставим в соответствие вершину и соединим две вершины ребром тогда и только тогда, когда соответствующие участки суши будут соединены мостом.

                       
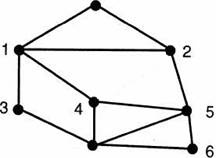
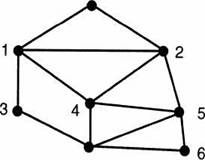
Рис 26                                                       рис. 27
Задача заключается в определении, будет ли граф Gэйлеровым. Найдем необходимые и достаточные условия существования эйлерова цикла.
Теорема 2. (Теорема Эйлера) Связный граф является эйлеровым тогда и только тогда, когда степень каждой его вершины четная.
Доказательство. Необходимость. Пусть G— эйлеров граф. Эйлеров цикл этого графа, проходя через каждую его вершину, входит в нее по одному ребру, а выходит по другому. Это означает, что каждое прохождение вершины по циклу вносит слагаемое 2 в ее степень. По­скольку цикл содержит все ребра графа, то степени всех вершин будут четными.
Достаточность.Предположим, что степени всех вершин связ­ного графа G четные. Начнем цепь G1 из произвольной вершины v1, и будем продлевать ее, выбирая каждый раз новое ребро. Так как степени вершин четные, то, попав в некоторую вершину, мы всегда будем иметь в распоряжении еще не пройденное ребро. Таким образом, построение це­пи Р1обязательно закончится в вершине v1, и Р1будет циклом. Если Р1содержит все ребра графа G, то построен эйлеров цикл. В противном слу­чае, удалив из Gребра Р1, получим граф G2. Так как степени всех вер­шин графов Gи Р1 были четными, то и G2будет обладать этим свойст­вом. В силу связности Gграфы Р1 и G2должны иметь хотя бы одну об­щую вершину v2. Теперь, начиная из v2, построим в G цикл Р2подобно тому, как построили Р1.
Объединим циклы Р1 и Р2следующим образом: пройдем часть Р1 от вершины v1 до вершины v2, затем пройдем цикл Р2, затем — оставшуюся часть Р1 от v2 до v1 (см. рис. 28).

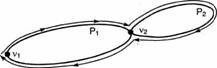
Рис. 28
Если объединенный цикл не эйлеров, то, проделав аналогичные построения, получим еще больший цикл. Поскольку степени вершин во всех графах, составленных из ребер, не попавших в строящийся цикл, четные, и число ребер в этих графах убывает, то процесс закончится по­строением эйлерова цикла. Теорема доказана.
Рассмотрим построенный граф G. В этом графе вершины 2 и 4 имеют нечетную степень, следовательно, граф G не является эйлеровым. Это означает, что желаемую прогулку по мостикам совершить нельзя.
Если же соединить ребром вершины 2 и 4, то степень всех вершин нового графа будет четной, а сам граф будет эйлеровым. Поэтому после постройки моста, соединяющего острова 2 и 4, можно найти маршрут прогулки по мостикам, начинающийся и заканчивающийся в одном мес­те, при котором каждый мостик будет пройден ровно один раз.
Докажем, что имеет место следующая теорема.
Теорема 3. Для уникурсального графа число вершин нечетного индекса равно нулю или двум.
Доказательство. Действительно, если граф уникурсален, то у него есть начало и конец обхода. Остальные вершины имеют четный индекс, так как с каждым входом в такую вершину есть и выход. Каждая пара вход – выход дает два ребра, сходящихся в данной вершине. Если начало и конец не совпадают, то они являются единственными вершинами нечетного индекса. У начала выходов на один больше, чем входов, а у конца входов на один больше чем выходов. Если же начало совпадает с концом, то вершин с нечетным индексом нет.
Теорема 4. Если граф G обладает эйлеровым путем c концами А и В (А не совпадает с В), то граф G связный и А и В — единственные нечетные его вершины.
Доказательство теоремы просим провести учеников.

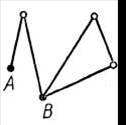
Рис. 29
Связность графа следует из опреде­ления эйлерова пути. Если путь начинается в А, а заканчивается в другой верши­не В, то и А и В — нечетные, даже если путь неоднократно про­ходил через А и В. В любую другую вершину графа путь должен был привести и вывести из нее, то есть все остальные вершины должны быть четными. Верно и обратное.
Теорема 5. Если граф G связный и А и В единственные нечетные вершины его, то граф G обладает эйлеровым путем с кон­цами А и В.
Доказательство:

Рис. 30
Вершины А и В могут быть соеди­нены ребром в графе (рис. 30), а могут быть и не соединены (рис. 29)

1. Если А и В соединены ребром, то удалим его; тогда все вершины станут четными. Новый граф, согласно предыдущей теореме, обла­дает эйлеровым циклом, началом и концом которого может служить любая вершина. Начнем эйлеров путь в вершине А и кончим его в вершине А. Добавим ребро (А, В) и получим эйлеров путь с на­чалом в А и концом в В.
2. Если А и B не соединены ребром, то к графу добавим новое ребро (А, В), тогда все вершины его станут четными. Новый граф, согласно предыдущей теореме, обладает эйлеровым циклом. Нач­нем его из вершины А по ребру (А, В). Закончится путь тоже в вершине А. Если удалить теперь из полученного цикла ребро (А, В), то останется эйлеров путь с началом в В и концом в А или с началом в А и концом в В.

Таким образом, всякую замкнутую фигуру, имеющую в точнос­ти две нечетные вершины, можно начертить одним росчерком без повторений, начав в одной из нечетных вершин, а кончив в другой.
Задача 4.2. «Муха в банке».
Муха забралась в банку из-под сахара. Банка имеет форму куба. Сможет ли муха последовательно обойти все двенадцать ребер куба, не проходя дважды по одному ребру. Подпрыгивать и перелетать с места на место не разрешается.

Решение. Является ли куб эйлеровым графом? Куб представляет собой граф, у которого все вершины имеют степень 3. Для того чтобы был эйлеровым нужно, чтобы все его вершины были четными, а это условие в данном случае не выполняется. Следовательно, граф не является эйлеровым. Значит, муха не сможет обойти все ребра куба, не проходя по одному ребру дважды.